Y@R3L!

miércoles, 16 de noviembre de 2011

Hipotesis , Louis-Victor De Broglie

Físico francés, Louis-Víctor de Broglie (1892-1987), formuló una hipótesis en la que afirmaba que:

* Toda la materia presenta características tanto ondulatorias como corpusculares comportándose de uno u otro modo dependiendo del experimento específico *

Http://youtu.be/dfpeprq7ogc

Para postular esta propiedad de la materia De Broglie se basó en la explicación del efecto fotoeléctrico, que poco antes había dado Albert Einstein sugiriendo la naturaleza cuántica de la luz. Para Einstein, la energía transportada por las ondas luminosas estaba cuantiada, distribuida en pequeños paquetes energía o cuantos de luz, que más tarde serían denominados fotones, y cuya energía dependía de la frecuencia de la luz a través de la relación: , donde es la frecuencia de la onda luminosa y la constante de Planck. Albert Einstein proponía de esta forma, que en determinados procesos las ondas electromagnéticas que forman la luz se comportan como corpúsculos. De Broglie se preguntó que por qué no podría ser de manera inversa, es decir, que una partícula material (un corpúsculo) pudiese mostrar el mismo comportamiento que una onda.

El físico francés relacionó la longitud de onda, λ (lambda) con la cantidad de movimiento de la partícula, mediante la fórmula:

Donde λ es la longitud de la onda asociada a la partícula de masa m que se mueve a una velocidad v, y h es la constante de Planck. El producto es también el módulo del vector, o cantidad de movimiento de la partícula. Viendo la fórmula se aprecia fácilmente, que a medida que la masa del cuerpo o su velocidad aumentan, disminuye considerablemente la longitud de onda.

Esta hipótesis se confirmó tres años después para los electrones, con la observación de los resultados del experimento de la doble rendija de Young en la difracción de electrones en dos investigaciones independientes. En la Universidad de Aberdeen, George Paget Thompson pasó un haz de electrones a través de una delgada placa de metal y observó los diferentes esquemas predichos. En los Laboratorios Bell, Clinton Joseph Davis son y Lester Halbert Germer guiaron su haz a través de una celda cristalina.

La ecuación de De Broglie se puede aplicar a toda la materia. Los cuerpos macroscópicos, también tendrían asociada una onda, pero, dado que su masa es muy grande, la longitud de onda resulta tan pequeña que en ellos se hace imposible apreciar sus características ondulatorias.

(MECANICA CUANTICA) Funcion de la onda

FUNCIÓN DE ONDA DE SCHRÖDINGER

Los descubrimientos de principios del Siglo XX habían culminado con la sorprendente conclusión, por parte de Louis de Broglie, de que la materia se comporta a la vez como cuerpo y como onda, y esto es especialmente decisivo cuando nos referimos a partículas subatómicas. Esta doble condición de las partículas tenía que ser utilizada para profundizar en el estudio del mundo de lo muy pequeño.

Así las cosas, Schrödinger, entre los años 1925 y 1926, introdujo la función de onda, también llamada ecuación de Schrödinger, que no es otra cosa que una ecuación que describe la forma en que una partícula cambia con el paso del tiempo. Por tanto, se trata de estudiar las partículas del mismo modo en que se estudian las demás ondas que sentimos a nuestro alrededor, como las sonoras o las producidas en el agua cuando se lanza una piedra a un charco.

Típica onda sobre el agua

Cualquier tipo de onda queda descrita en cualquier instante mediante una lista de números, un número por cada punto del espacio por el que viaja la onda. Por ejemplo, en el caso de la onda sonora, lo números nos darán la presión del aire en cada punto del espacio (porque es el aire quien transmite el sonido). Otro caso cotidiano es la onda que produce un músico sobre la cuerda de una guitarra cuando la hace sonar, la cual estaría descrita por números que nos darían la tensión de dicha cuerda en cada uno de sus puntos.

Y del mismo modo, la función de onda de las partículas nos da números concernientes a estas partículas. La peculiaridad de estos números es que son probabilidades, es decir, el valor de la función de onda en cualquier punto nos da la probabilidad de que la partícula se halle en ese punto.

Esquema de una función de onda
monoelectrónica u orbital en dos
dimensiones.

_____________________________

Formula:

En 1923 De Broglie propuso la llamada hipótesis de De Broglie por la que a cualquier partícula podía asignársele un paquete de ondas materiales o superposición de ondas de frecuencia y longitud de onda asociada con el momento lineal y la energía:

$p = \frac{h}{\lambda} = \hbar k \qquad E_k = h\nu = \hbar \omega$

donde $p,\ E_k\;$ son el momento lineal y la energía cinética de la partícula, y $k,\omega \;$ son el vector número de onda y la frecuencia angular. Cuando se consideran partículas macroscópicas muy localizadas el paquete de ondas se restringe casi por completo a la región del espacio ocupada por la partícula y, en ese caso, la velocidad de movimiento de la partícula no coincide con la velocidad de fase de la onda sino con la velocidad de grupo del paquete:

$v_g = \frac{\partial \omega}{\partial k} = \frac{\partial E_k}{\partial p} = \frac{\partial E_k(p)}{\partial p} = \frac{p}{m}$

donde

E k (p) = P 2 / 2 m

. Si en lugar de las expresiones clásicas del momento lineal y la energía se usan las expresiones relativistas, lo cual da una descripción más precisa para partículas rápidas, un cálculo algo más largo, basado en la velocidad de grupo, lleva a la misma conclusión.

La fórmula de De Broglie encontró confirmación experimental en 1927 un experimento que probó que la ley de Bragg, inicialmente formulada para rayos X y radiación de alta frecuencia, era también válida para electrones lentos si se usaba como longitud de onda la longitud postulada por De Broglie. Esos hechos llevaron a los físicos a tratar de formular una ecuación de ondas cuántica que en el límite clásico macroscópico se redujera a las ecuaciones de movimiento clásicas o leyes de Newton. Dicha ecuación ondulatoria había sido formulada por Erwin Schrödinger en 1925 y es la celebrada Ecuación de Schrödinger:

$-{\hbar^2\over 2m} \nabla^2 \psi (x,t) + V(x)\psi (x,t) = i \hbar {\partial \psi (x,t)\over\partial t}$

donde $\psi(x,t)\,$ se interpretó originalmente como un campo físico o campo de materia que por razones históricas se llamó función de onda y fue el precedente histórico del moderno concepto de función de onda.

El concepto actual de función de onda es algo más abstracto y se basa en la interpretación del campo de materia no como campo físico existente sino como amplitud de probabilidad de presencia de materia. Esta interpretación, introducida por Max Born, le valió la concesión del premio Nobel de física en 1954.

______________________________________________

Formulación moderna de Von Neumann

La formalización rigurosa de la función de onda requiere considerar espacios de Hilbert equipados, donde puedan construirse bases más generales. Así para cualquier operador autoadjunto, al teorema de descomposición espectral, permite construir el equivalente de una base vectorial dependiente de un índice continuo (infinito, incontable). Por ejemplo, si se considera el operador de posición $\hat{\mathbf{X}}$ , que es autoadjunto sobre un dominio denso en el espacio de Hilbert convencional $\mathcal{H} \approx L^2(\R^n)$ , entonces se pueden construir estados especiales:

$| \mathbf{x} \rangle \notin \mathcal{H} \qquad \hat{\mathbf{X}}| \mathbf{x} \rangle = \mathbf{x}| \mathbf{x} \rangle \in \mathcal{H}_e \qquad \mathcal{H} \subset \mathcal{H}_e$

Pertenecientes a un espacio equipado de Hilbert $\mathcal{H}_e$ , tal que la función de onda puede ser interpretada como las "componentes" del vector de estado del sistema respecto a una base incontable formada por dichos vectores:

$| \psi \rangle = \int_{-\infty}^{\infty} \psi(\mathbf{x}) | \mathbf{x} \rangle\,d\mathbf{x}$

Nótese que aunque los estados propios $| \mathbf{x} \rangle$ del operador posición $\hat{\mathbf{X}}$ no son normalizables, ya que en general no pertenecen al espacio de Hilbert convencional del sistema (sino sólo al espacio equipado), el conjunto de funciones de onda sí definen estados en el espacio de Hilbert. Eso sucede porque los estados propios satisfacen:

$| \mathbf{x} \rangle, | \mathbf{x}' \rangle \in \mathcal{H}_e \qquad \langle \mathbf{x} | \mathbf{x}' \rangle = \delta(\mathbf{x}-\mathbf{x}')$

Puesto que las funciones de onda así definidas, que son de cuadrado integrable, sí forman un espacio de Hilbert isomorfo y homeomorfo al original, el cuadrado del módulo de la función de onda puede ser interpretado como la densidad de probabilidad de presencia de las partículas en una determinada región del espacio.

Un tratamiento análogo al anterior usando vectores propios del operador momento lineal $\hat{\mathbf{P}}$ también pertenecientes a un espacio equipado de Hilbert permiten definir las "funciones de onda" sobre el espacio de momentos. El conjunto de estos estados cuánticos propios del operador momento son llamados en física "base de espacio-k" (en contraposición a la función de onda obtenida a partir del operador posición que se llama "base de espacio-r"). Por la relación de conmutación entre los Operador (mecánica cuántica)operadores posición y momento, las funciones de onda en espacio-r y en espacio-k son pares de transformadas de Fourier.

$\tilde\psi(\mathbf{p}) = \frac{1}{(2\pi\hbar)^{3/2}} \int_{\R^3} \psi(\mathbf{x}) e^{- i\mathbf{p}\cdot\mathbf{x}/\hbar}\,d\mathbf{x}$

El nombre espacio-k proviene de que $\mathbf{p} = \hbar\mathbf{k}$ , mientras que el nombre espacio-r proviene del hecho de que las coordenadas espaciales con frecuencia se designan mediante el vector $\mathbf{r}$

miércoles, 9 de noviembre de 2011

* MODELO ATONMICO DE BOHR" "LA MECÁNICA CUÁNTICA"

BOHR trabajó con Rutherford cuando este ya había postulado su modelo. Postuló un modelo sin demostración experimental que lo demostrara. Se suele decir de él que soñó con el modelo una noche y a la mañana siguiente lo escribió con la suerte de que sus ideas eran las correctas y el modelo perdura en el tiempo.

Los electrones giran en órbitas circulares (esto es lo Único que no se mantiene actualmente) en torno al Núcleo merced a la atracción eléctrica protón-electrón.

Modelo atómico de bohr.

El electrón no puede situarse a cualquier distancia del núcleo, sino que debe ocupara niveles u órbitas predeterminadas. no valen posiciones intermedias entre órbitas

Mientras el electrón se mueve en su órbita no pierde energía. Si pasa de una órbita externa a otra más interna desprende energía, la misma que absorbe para la transición contraria.

Modelo atómico de Bohr

El modelo de Bohr es muy simple y recuerda al modelo planetario de Copérnico, los planetas describiendo órbitas circulares alrededor del Sol. El electrón de un átomo o ión hidrogenoide describe también órbitas circulares, pero los radios de estas órbitas no pueden tener cualquier valor.

Consideremos un átomo o ión con un solo electrón. El núcleo de carga Ze es suficientemente pesado para considerarlo inmóvil,

En el modelo de Bohr, solamente están permitidas aquellas órbitas cuyo momento angular está cuantizado.n

Los radios de las órbitas permitidas son

donde a₀ se denomina radio de Bohr. a₀ es el radio de la órbita del electrón del átomo de Hidrógeno Z=1 en su estado fundamental n=1.

La energía total es

En una órbita circular, la energía total E es la mitad de la energía potencial

La energía del electrón aumenta con el número cuántico n.

La primera energía de excitación es la que lleva a un átomo de su estado fundamental a su primer (o más bajo) estado excitado. La energía del estado fundamental se obtiene con n=1, E₁= -13.6 eV y la del primer estado excitado con n=2, E₂=-3.4 eV. Las energías se suelen expresar en electrón-voltios (1eV=1.6 10^-19 J)

La frecuencia f de la radiación emitida cuando el electrón pasa del estado excitado E₂ al fundamental E₁ es:

Los sistemas atómicos y las partículas elementales no se pueden describir con las teorías que usamos para estudiar los cuerpos macroscópicos (como las rocas, los carros, las casas, etc). Esto de debe a un hecho fundamental respecto al comportamiento de las partículas y los átomos que consiste en la imposibilidad de medir todas sus propiedades simultáneamente de una manera exacta. Es decir en el mundo de los átomos siempre existe una INCERTIDUMBRE que no puede ser superada. La mecánica cuántica explica este comportamiento.

_________________________________________________

La Mecanica Cuantica.

¿EN QUÉ CONSISTE LA MECÁNICA CUÁNTICA?

La Mecánica cuántica es la parte de la física que estudia el movimiento de las partículas muy pequeñas. El concepto de partícula "muy pequeña" atiende al tamaño en el cual comienzan a notarse efectos como la imposibilidad de conocer con exactitud infinita y a la vez la posición y la velocidad de una partícula (véase Principio de indeterminación de Heisenberg), entre otros. A tales efectos suele denominárseles "efectos cuánticos". Así, la Mecánica cuántica es la que rige el movimiento de sistemas en los cuales los efectos cuánticos sean relevantes. Se ha documentado que tales efectos son importantes en materiales mesoscópicos (unos 1.000 átomos).
Las suposiciones más importantes de esta teoría son las siguientes:

La energía no se intercambia de forma continua, sino que en todo intercambio energético hay una cantidad mínima involucrada.

Al ser imposible fijar a la vez la posición y la velocidad de una partícula, se renuncia al concepto de trayectoria, vital en Mecánica clásica. En vez de eso, el movimiento de una partícula queda regido por una función matemática que asigna, a cada punto del espacio y a cada instante, la probabilidad de que la partícula descrita se halle en tal posición en ese momento (al menos, en la interpretación de la Mecánica cuántica más usual, la probabilística o "de Copenhagen"). A partir de esa función, o función de onda, se extraen teóricamente todas las magnitudes del movimiento necesarias.

Aunque la estructura formal de la teoría está bien desarrollada, no sucede lo mismo con su interpretación, que sigue siendo objeto de controversias.
La teoría cuántica fue desarrollada en su forma básica a lo largo de la primera mitad del siglo XX. El hecho de que la energía se intercambiaba de forma discreta se puso de relieve por hechos experimentales como los siguientes:

Espectro de la radiación del Cuerpo negro, resuelto por Max Planck con la cuantización de la energía.

Explicación del efecto fotoeléctrico, dada por Albert Einstein, en que volvió a aparecer esa "misteriosa" necesidad de cuantizar la energía.

Efecto Compton.

¿ENTONCES QUÉ DICE LA MECÁNICA CUÁNTICA?

E l tamaño de un núcleo atómico es del orden de 10^-13 centímetros. ¿Podemos imaginar ésto? Muy difícilmente. Mucho más difícil aún sería imaginar como interactúan dos núcleos atómicos, o cómo interactúa el núcleo con los electrones en el átomo. Por eso lo que dice la mecánica cuántica muchas veces nos parece que no es 'lógico'. Veamos que propone la mecánica cuántica:

El intercambio de energía entre átomos y partículas solo puede ocurrir en paquetes de energía de cantidad discreta (Fuerzas e Interacciones)
Las ondas de luz, en algunas circunstancias se pueden comportar como si fueran partículas ( fotones).

Las partículas elementales, en algunas circunstancias se pueden comportar como si fueran ondas.

Es imposible conocer la posición exacta y la velocidad exacta de una partícula al mismo tiempo. Este es el famoso Principio de Incertidumbre de Heisemberg

LA TEORÍA CUÁNTICA

Según la teoría clásica del electromagnetismo la energía de un cuerpo caliente sería infinita!!!

Esto es imposible en el mundo real, y para resolver este problema el físico Max Plank inventó la mecánica cuántica.

es un número entero que se denomina número cuántico, y h es la constante de Planck 6.6256·10^-34 Js

miércoles, 2 de noviembre de 2011

RADIACION DE UN CUERPO NEGRO

Equipo 5: Blanca, Noeemyy, Rubí y Nestor. Tema: Teoría cuántica: radiación de un cuerpo negro y el efecto fotoeléctrico.

http://www.youtube.com/watch?v=IfkWSqyl9qs&feature=related

Radiación de un cuerpo negro

El término radiación se refiere a la emisión continua de energía desde la superficie de cualquier cuerpo, esta energía se denomina radiante y es transportada por las ondas electromagnéticas que viajan en el vacío a la velocidad de 3·10⁸ m/s . Las ondas de radio, las radiaciones infrarrojas, la luz visible, la luz ultravioleta, los rayos X y los rayos gamma, constituyen las distintas regiones del espectro electromagnético.

Propiedades de la superficie de un cuerpo

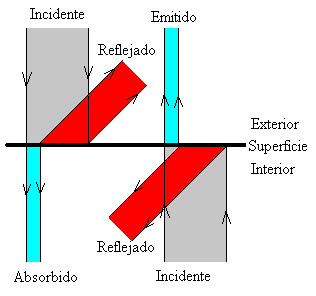
Sobre la superficie de un cuerpo incide constantemente energía radiante, tanto desde el interior como desde el exterior, la que incide desde el exterior procede de los objetos que rodean al cuerpo. Cuando la energía radiante incide sobre la superficie una parte se refleja y la otra parte se transmite. Consideremos la energía radiante que incide desde el exterior sobre la superficie del cuerpo. Si la superficie es lisa y pulimentada, como la de un espejo, la mayor parte de la energía incidente se refleja, el resto atraviesa la superficie del cuerpo y es absorbido por sus átomos o moléculas.

Si r es la proporción de energía radiante que se refleja, y a la proporción que se absorbe, se debe de cumplir que r+a=1.

La misma proporción r de la energía radiante que incide desde el interior se refleja hacia dentro, y se transmite la proporción a=1-r que se propaga hacia afuera y se denomina por tanto, energía radiante emitida por la superficie.

En la figura, se muestra el comportamiento de la superficie de un cuerpo que refleja una pequeña parte de la energía incidente. Las anchuras de las distintas bandas corresponden a cantidades relativas de energía radiante incidente, reflejada y transmitida a través de la superficie.

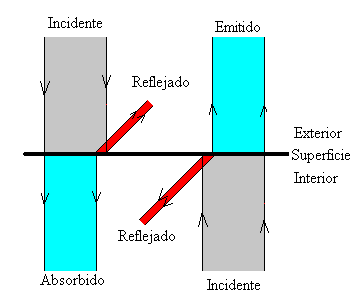
Comparando ambas figuras, vemos que un buen absorbedor de radiación es un buen emisor, y un mal absorbedor es un mal emisor. También podemos decir, que un buen reflector es un mal emisor, y un mal reflector es un buen emisor.

Cuerpo negro

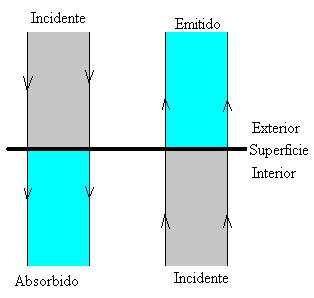
La superficie de un cuerpo negro es un caso límite, en el que toda la energía incidente desde el exterior es absorbida, y toda la energía incidente desde el interior es emitida.

No existe en la naturaleza un cuerpo negro, incluso el negro de humo refleja el 1% de la energía incidente.

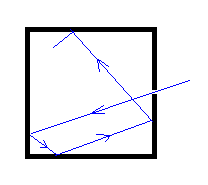
Sin embargo, un cuerpo negro se puede sustituir con gran aproximación por una cavidad con una pequeña abertura. La energía radiante incidente a través de la abertura, es absorbida por las paredes en múltiples reflexiones y solamente una mínima proporción escapa a través de la abertura. Podemos por tanto decir, que toda la energía incidente es absorbida.

Efecto fotoeléctrico

El efecto fotoeléctrico consiste en la emisión de electrones por un metal cuando se hace incidir sobre él una radiación electromagnética. A veces se incluyen en el término otros tipos de interacción entre la luz y la materia:

Foto conductividad: es el aumento de la conductividad eléctrica de la materia o en diodos provocada por la luz. Descubierta por Willoughby Smith en el selenio hacia la mitad del siglo XIX.
Efecto foto voltaico: transformación parcial de la energía luminosa en energía eléctrica. La primera célula solar fue fabricada por Charles Fritts en 1884. Estaba formada por selenio recubierto de una fina capa de oro.

Sus características esenciales son:

Para cada sustancia hay una frecuencia mínima o umbral de la radiación electromagnética por debajo de la cual no se producen fotoelectrones por más intensa que sea la radiación.

La emisión electrónica aumenta cuando se incrementa la intensidad de la radiación que incide sobre la superficie del metal, ya que hay más energía disponible para liberar electrones.

Descripción

Sea f la energía mínima necesaria para que un electrón escape del metal. Si el electrón absorbe una energía E, la diferencia E-f, será la energía cinética del electrón emitido.

Einstein explicó las características del efecto fotoeléctrico, suponiendo que cada electrón absorbía un cuanto de radiación o fotón. La energía de un fotón se obtiene multiplicando la constante h de Planck por la frecuencia f de la radiación electromagnética.

E=hf

Si la energía del fotón E, es menor que la energía de arranque f, no hay emisión fotoeléctrica. En caso contrario, si hay emisión y el electrón sale del metal con una energía cinética E_k igual a E-f.

Por otra parte, cuando la placa de área S se ilumina con cierta intensidad I, absorbe una energía en la unidad de tiempo proporcional a IS, basta dividir dicha energía entre la cantidad hf para obtener el número de fotones que inciden sobre la placa en la unidad de tiempo. Como cada electrón emitido toma la energía de un único fotón, concluimos que el número de electrones emitidos en la unidad de tiempo es proporcional a la intensidad de la luz que ilumina la placa

MASA Y ENERGIA

Equipo 4: Eduardo Gpe, Edgar Eduardo y Eric Eduardo. Tema: Masa y Energía relativista.

http://dl.dropbox.com/u/38669735/Experimento.3gp

Masa y Energía relativista:

La masa es una de las magnitudes fundamentales de la física.
La masa de una estrella De hecho, muchos fenómenos de la naturaleza están, directa o indirectamente, asociados al concepto de masa.
La energía es una propiedad asociada a los objetos y sustancias y se manifiesta en las transformaciones que ocurren en la naturaleza.
La energía se manifiesta en los cambios físicos, por ejemplo, al elevar un objeto, transportarlo, deformarlo o calentarlo.

Un primer acercamiento al concepto de masa se puede expresar al decir que “masa es la cantidad de materia que tiene un cuerpo”.

La energía total relativista (E) es una propiedad de todo sistema físico, masivo o no masivo, cuyo valor aumenta (disminuye) cuando se le entrega (quita) energía por cualquier proceso, y toma el valor cero sólo cuando el sistema se aniquila (desaparece). En consecuencia, para un determinado sistema de referencia inercial, su valor depende del estado del sistema físico y sólo será constante si el sistema físico está aislado. Resulta evidente, además, que la magnitud Energía total es relativa al sistema de referencia.

Tanto la visión de Newton como la de Einstein se basaron en una descripción física y matemática de la Realidad. Ahora bien, si Newton partía de los cuerpos (del qué, de la materia como primordialidad), Einstein puso su atención, sobre todo, en los fenómenos, a los que dedicó los primeros Postulados de la relatividad especial.

FISICA RELATIVISTA RELATIVIDAD GALILEANA Y ECUECION DE LORENTZ-FITZGERALD

Equipo 3: Guillermo, Irving R. y Roberto. Tema: Física relativista: relatividad galileana y ecuación de Lorentz-Fitzgerald

http://dl.dropbox.com/u/41022376/MOV00050.3gpFisica relativista.

Las ecuaciones del electromagnetismo exhiben caracteristicas novedosas respecto a la fisica newtoniana. La fuerza de Lorentz, debido al termino q~u ^ ~B depende del sistema inercial desde donde se observa el fenomeno. Asi mismo, en las ecuaciones de Maxwell aparece una constante con dimensiones de velocidad, c. Como se demuestra en la seccion relativa a ondas electromagneticas, c es la velocidad de propagacion de dichas ondas en el vacio. Es obvio que esta velocidad, analizada desde el punto de vista prerelativista, debe depender del sistema de referencia inercial. Esto esta en contra del un Principio de Relatividad (PR) asumido por la fisica clasica: Cualquier fenomeno obedece leyes iguales en todos los triedros inerciales. Como vemos, la leyes del electromagnetismo parecen sugerir la existencia de un triedro de referencia especial , el eter, con lo que se viola el (PR). Sin embargo, la evidencia experimental indica que tal eter no existe, y en consecuencia c es un valor universal independiente del triedro inercial de referencia. El Principio de Relatividad de Einstein22 (PRE) indica que se cumplen ambos, el (PR) y que c es constante para todo sistema inercial. Esto modifica las relaciones entre distancias e intervalos de tiempos, entre otras, con respecto a la fisica prerelativista.

El principio de la relatividad galileana establece que:

‘Dos sistemas de referencia en movimiento relativo de traslación rectilínea uniforme son equivalentes desde el punto de vista mecánico; es decir, los experimentos mecánicos se desarrollan de igual manera en ambos, y las leyes de la mecánica son las mismas.’

POLARIZACION Y RADIACION LASER

Equipo 2: César, Daniela, Itsel y Brenda G.

Polarización y radiación láser:

http://dl.dropbox.com/u/38770069/Polarization%20%5Bwww.bajaryoutube.com%5D.mp4

Polarización de la luz

Las ondas luminosas no suelen estar polarizadas, de forma que la vibración electromagnética se produce en todos los planos. La luz que vibra en un solo plano se llama luz polarizada.

Supongamos un dispositivo experi mental consistente en dos polarizadores superpuestos (polarizador y analizador), de forma que un haz de luz los atraviese, y que uno de ellos puede girar respecto del otro, que permanece estático. La intensidad luminosa transmitida por el sistema variará con el ángulo de giro, de tal manera que pasará por dos puntos de máxima luminosidad separados 180º, con dos puntos de oscuridad total a 90º de los anteriores. Entre estos extremos la intensidad va creciendo y decreciendo paulatinamente, según los casos.

Este fenómeno de polarización solo se da con ondas transversales, pero no con longitudinales, ya que implica una asimetría respecto del eje en la dirección de propagación. Si se demuestra que un haz luminoso puede ser polarizado, llegaremos a la conclusión de que las ondas luminosas son transversales.

La luz emitida por un manantial está constituida por una serie de trenes de ondas procedentes de átomos distintos; en cada uno de estos trenes de ondas el campo eléctrico oscila en un plano determinado pero, en general, su orientación es distinta de unos a otros. Dado el enorme número de moléculas y átomos de un manantial luminoso, se comprende el gran número de trenes de ondas que constituye un haz de luz y, por consiguiente, la existencia en éste de ondas polarizadas en todas las direcciones transversales posibles.

Veamos algunos casos en los que se produce polarización de la luz.

Polarización por reflexión.

Sabemos que si sobre una superficie reflectora incide luz natural parte de la luz se refleja y parte se refracta. Malus descubrió en 1808 que si hacemos incidir una luz sobre una superficie pulimentada de vidrio con un ángulo de incidencia i de 57º aproximadamente, la luz reflejada está polarizada, siendo el plano de vibración perpendicular al plano de incidencia de los rayos. Si el ángulo de incidencia no es de 57º habrá también polarización pero será menor a medida que el rayo incidente vaya siendo mayor o menor que dicho ángulo.

Más tarde Brewster descubrió que si el rayo reflejado y el refractado forman entre si un ángulo de 90º, el ángulo de incidencia es precisamente el ángulo de polarización. El ángulo de polarización depende del índice de refracción "n" del medio.

En el caso del vidrio, que acabamos de ver, el ángulo es aproximadamente 57º. Hay que señalar también que para este ángulo, el rayo refractado está polarizado parcialmente, coincidiendo su plano de vibración con el de incidencia, mientras que el rayo reflejado está completamente polarizado.

Polarización por doble refracción.

Hay determinados cristales que tienen la propiedad de la doble refracción, es decir, el rayo incidente se desdobla en dos en el interior del cristal (espato de islandia, turmalina), uno de ellos llamado ordinario y que sigue las leyes de la refracción y otro llamado extraordinario que no las sigue.

Este tipo de cristal permite obtener luz polarizada partiendo de la luz natural, siempre que logremos eliminar a la salida uno de los rayos emergentes. Esto se puede conseguir con un prisma de Nicol, constituido por un cristal de espato de Islandia al que se le han cortado las caras externas de manera que el ángulo de 71º pase a ser de 68º, después se corta la diagonal, obteniéndose dos prismas que se pegan con bálsamo de Canadá, cuyo índice de refracción está entre el indice de refracción del rayo ordinario y el del extraordinario. En estas condiciones el rayo ordinario sufre reflexión total al llegar a la lámina de bálsamo de Canadá, mientras que el extraordinario se refracta en el bálsamo y se transmite a través del segundo prisma.

Radiación laser

§La palabra LÁSER es un acrónimo de la expresión inglesa Light Amplification by Stimulated Emission of Radiation (luz amplificada por emisión estimulada de radiación).

§Las aplicaciones de la radiación láser superan cualquier expectativa
y ya constituyen herramientas insustituibles
en las investigaciones científicas, la industria y la medicina.

§La radiación láser es la radiación electromagnética emitida por un producto láser en el intervalo de longitudes de onda comprendido entre 180 nm y 1 mm, que es radiada como resultado de la emisión estimulada de luz.

§El intervalo de longitudes de onda comprendidas entre 180 nm y 1 mm, engloba a la radiación ultravioleta, la radiación visible y la radiación infrarroja en la secuencia siguiente:

180 - 400 nm - ultravioleta

400 - 700 nm - visible

700 nm - 1 mm - infrarrojo

El nivel de radiación láser al que las personas pueden estar expuestas en circunstancias normales, sin sufrir efectos adversos, se denomina exposición máxima permisible (EMP). Los niveles de EMP representan el nivel máximo al cual el ojo o la piel pueden resultar expuestos sin sufrir los daños derivados de la exposición ni inmediatamente ni después de un período largo de tiempo, estando tales niveles relacionados con la longitud de onda de la radiación, la duración del impulso o el tiempo de exposición, el tejido expuesto al riesgo y el tamaño de la imagen sobre la retina.